Python五作：模拟人工解法计算数独

程序说明

本程序根据用户输入的谜局，计算出解决方法。
注意：目前只能解决可以用唯一候选数法解决的数独谜局。

操作说明

按行输入谜局，空格用英文或数字状态下的空格，或者数字0来输入。每行输入完后按回车。
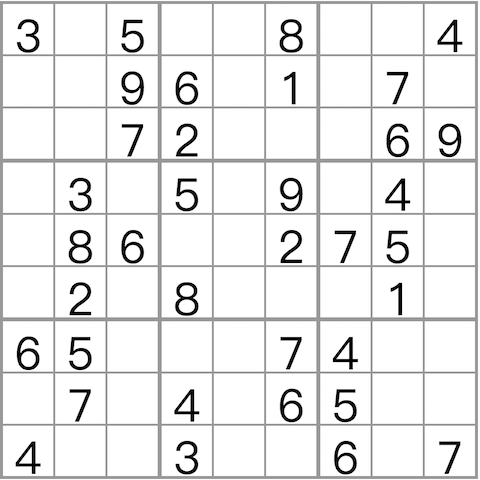
例如要输入以下这个谜局：

则按行输入：

（以数字 0 隔开，方便看清间隔，不容易填错）  
305008004
009601070
007200069
030509040
086002750
020800010
650007400
070406500
400300607 
（或以空格隔开，把上面的“0”用“ ”代替）

相关配置

我在6670上完美运行，如果你无法正常运行，可以考虑安装如下相关软件（选择你自己手机版本的平台）
我的机型是诺基亚6670，Python平台环境如下：

• PythonForS60_1_4_0_2ndEd
• PythonScriptShell_1_4_0_2ndEd
• Ped_1.67_2ndEd

相关原理

R.E.S证明了数独谜题是NP问题。
更准确地说，数独是NPC问题。
其中，NP就是Non-deterministic Polynomial，即多项式复杂程度的非确定性问题。NPC即NP完全问题（C代表complete）。图论中著名的哈米尔顿回路问题就是一个NPC问题。

五作手记

数独（Sudoku）这个游戏我很早就有耳闻，后来CP论坛也开始有人提到了，但是我一直不感冒，没有去尝试过。前几天在图书馆看我最喜欢的数码杂志，居然有三份杂志都提到数独，其中有一份还有每期数独解谜栏目。这下触动了我，回来就下了游戏来玩。到目前为止，极易级的最好是6分41秒搞定，中级的还一个迷题都没解开过-_-|| 不过我已经相信这是不错的游戏了——因为我比较喜欢智力型游戏，而且不用太多击键，这对保护我小6来说可是好事～～

正如我一贯的作风一样——玩单机游戏我很难耐住性子，基本上很快就要去找攻略来看——我google了一下关于数独的解决办法，正如上文“相关原理”所说，既然知道了一个问题的数学模型，事实上用编程解决它已经有希望了，于是我着手编制这个程序。

处理这个问题我马上能想到三种方法：1.穷举法 2.回溯法 3.模拟人工解法

其中，穷举法极端情况是10的77次方的数量级（事实上比这个数字小得多，但仍然要N多次循环），直接放弃。

回溯法是解决NPC问题的常规方法，网上能找到的java/c++/pascal版本等解数独程序普遍是回溯法。相较穷举法，回溯效率高很多了，但毕竟极端情况还是81层（事实上应该排除已知数字的层）。改进的回溯是应用快速剪枝。但是因为回溯法本身的限制，针对数独来说它绝对不是高效率算法。

最后，我们开始来探讨模拟人工解法。这是显然的效率最高，当然工程量也最大的算法。
一般的人工解法流程：

1. 根据行、列和区块的限制条件排除不可能的候选字，把剩下的候选字逐一填入空白的格子
2. 审视第一步骤的结果，如果发现某个空格只有一个数字，即确定该空格为这个数字。并根据该数字审视其相关的行、列和区块，并划除相同的数字。（该情况出现的可能往往不多，除了较简单的数独题，但这是一个必要的过程，而且在随后的过程中要反复使用此方法。）
3. 审视各个行、列和区块中罗列出的可能的数字结果，若发现某一个数字在各个行、列或区块中出现的次数仅一次，则可以确定该空格的解为此数字。并根据第二条的方法排除与此空格相关列或方格中相同的数字。
4. 审视各个行、列和区块中罗列的各个可能的结果，找出相对称的两个数组合的空格（或3个、4个组合），并确定这两个空格（或3个、4个）的数字只可能为这两个数字，即两个数字在这两个空格的位置可以交换，但不可能到该行、该列或该区块的其他位置。根据此结果可以排除相关列或区块罗列出相关数字的可能，并缩小范围。（该步骤处理的难度相对复杂，需要在积累一定经验的基础上进行，也是最终求解的关键）
5. 反复使用2、3、4提到的步骤，逐步得到一个一个空格的解，并将先前罗列的各种可能的结果一个一个排除，使可能的范围越来越小，直至得到最后结果。

其中，第1、2、3步我都已经用程序实现，但是第4步我还没有完成，可以考虑的方法是用并查集查找，现实的程序还在构思中……工程量……比较大……

只用1、2、3步，已经能够解决可以用唯一候选数法解决的数独谜局。一般极易级的题目大都能搞定。

用回溯法（不考虑快速剪枝）解数独，代码量很少，而且也没什么难度。这让我想起一些言论。总有人会说，电脑很笨，它唯一的优点就是速度快。可是电脑为什么笨？那是因为你没有找到高效率的算法而已！对于普通用户来说，确实，1秒钟搞定和0.1秒甚至0.01秒搞定没有什么区别。但是程序员也这样考虑问题的话，我想科技就不会进步了。

附件

[附件]